Двоичные деревья

Деревья — это структуры данных, которые состоят из узлов, хранящих данные. У каждого узла есть ссылки на несколько дочерних узлов, и на каждый узел кроме одного, называемого корневым, есть ровно одна ссылка.

В двоичном дереве у каждого узла не может быть более двух дочерних. Пример двоичного дерева виден на картинке:

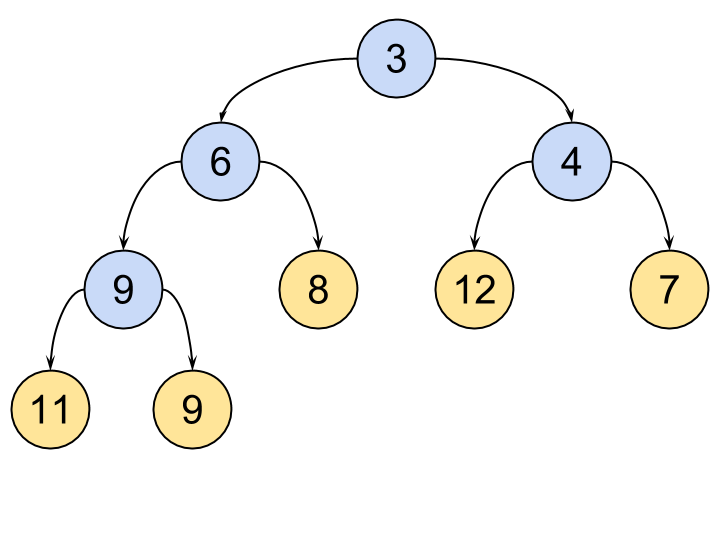
Обычно узлы хранятся в виде структуры:

class/struct Node
    value — значение в узле
    left: Node — ссылка на первый дочерний узел или ничего
    right: Node — ссылка на второй дочерний узел или ничего

А само дерево — это root: Node — т.е. ссылка на корень.

Двоичные деревья бывают разные для разных целей.

Двоичные деревья поиска хранят упорядоченное множество объектов, например, хранят множество чисел, и позволяют

• добавлять, удалять элементы
• проверять, есть ли элемент в множестве
• искать минимальные, максимальные элементы множества
• перечислять элементы множества в порядке возрастания или убывания.
• находить для заданного элемента следующий по порядку, или предыдущий.

Если вы знакомы с хэш-таблицами, то можете сравнить с ними двоичные деревья поиска. Предположим, что значения в узлах дерева состоят из двух частей. Ключей, по которым упорядочиваются узлы, и дополнительных значений. Тогда двоичное дерево позволяет совершать те же действия, что и хэш таблица: искать значения по ключам. Но, в отличие от хэш таблиц, деревья поиска знают о порядке элементов множества.

Куча — еще один вид двоичных деревьев. Они имеют ограниченный набор операций в сравнении с деревьями поиска, зато значительно проще реализуются. В куче можно добавлять элементы в множество, находить минимальный, удалять минимальный. Куча используется в основном как очередь с приоритетами. Это структура данных, похожая на очередь. При добавлении элемента в очередь с приоритетом у него указывается приоритет, и при извлечении элемента из очереди извлекается тот, у которого самый высокий приоритет. Еще с помощью кучи можно сортировать элементы массива, хотя это и не самый распространенный алгоритм сортировки.

Сбалансированные двоичные деревья поиска. Если программировать двоичное дерево поиска наивно, без оптимизаций, оно может работать очень неэффективно. Чтобы операции поиска элемента, добавления, удаления гарантированно работали эффективно, нужно, чтобы дерево было сбалансированным. Это означает, что у каждого узла левые и правые поддеревья должны быть примерно одинакового размера. Есть очень много подходов к тому, как балансировать деревья. Возможно, вы слышали об АВЛ-деревьях, красно-черных деревьях и других вариантах деревьев. Такие деревья после каждого изменения балансируются разными способами, чтобы гарантировать эффективную работу. Но их довольно трудно программировать из-за необходимости разбирать больше число случаев того, как могла нарушиться балансировка.

В этом курсе я предлагаю реализовать Декартово дерево. Его особенность в том, что его очень легко программировать, все операции занимают буквально несколько строчек. Для тех, кто участвует в соревнованиях, где нельзя пользоваться стандартной библиотекой со структурами данных, такое дерево незаменимо. Подвох с этим деревом только в том, что оно использует случайные числа, и, хоть и с очень небольшой вероятность, может выполнять запрос долго. На практике этими вероятностями можно пренебречь.

Задания про двоичные деревья

Двоичная куча

Тесты tests.zip

Решайте эту задачу, только если вы раньше не программировали кучу. Реализация кучи на основе массива

В первой строке входа дано число N, после него следует N строк с командами для двоичной кучи. Необходимо начать с пустой кучи. Если в строке написано число, нужно добавить его в кучу. Если в строке написано GET, нужно написать в выходной файл текущий максимальный элемент кучи и удалить его из кучи.

Например, для входа

11
10
30
GET
40
20
60
10
GET
GET
0
GET

будет выведено

30
60
40
20

Двоичные деревья поиска

Эту задачу можно решать для разных двоичных деревьев:

1. Двоичное дерево поиска, наивная реализация без оптимизаций: материалы про наивную реализацию
2. Декартово дерево: материалы про декартово дерево
3. Дерево из стандартной библиотеки вашего языка. Найдите у себя в языке такое дерево и воспользуйтесь им для решения задачи.

Реализуйте те деревья, которые сами считаете нужным. Я рекомендую реализовать пункт 3 всем, чтобы познакомиться со стандартной библиотекой своего языка. 1 я рекомендую только тем, кто этого не делал. 2 рекомендую всем, у кого осталось на это время после решения других задач.

Тесты

Только проверка на вхождение элемента

В стандартном входе в первой строке написано число N, оно означет количество чисел, которые будут даны дальше для добавления в двоичное дерево. Заведите пустое двоичное дерево поиска. Дальшее в N строках находится по одному числу. Для каждого числа вы сначала проверяете, было ли это число в дереве, а потом добавляете число в дерево, если его не было. В вывод в отдельную строку нужно написть + или - в зависимости от того, было ли число в дереве. Т.е., встречалось ли оно раньше. Например, для входа 4 10 20 10 30 (в примере всё в одну строку) вы должны вывести - - + -.

Для проврки файлы с тестами заканчиваются на слово contains, например, 1.contains.out.

Поиск следующего элемента

Задача аналогична предыдущей, но кроме знака + или - в строку надо вывести следующее по порядку число за вставленным. Или -, если такого числа нет. Например, для входа 5 20 10 20 40 30 (в примере всё в одну строку) вы должны вывести

- - (потому что 20 еще нет)
- 20 (потому что сразу за 10 в дереве идет число 20 по порядку)
+ - (число 20 есть, но следующего по порядку за ним нет)
- -
- 40 (числа 30 нет, но по порядку за ним идет 40)

Для проверки файлы с тестами заканчиваются на слово min-after, например, 1.min-after.out.